前言
在比赛结束后一小时,得出了最终结果——

怎么说呢,虽然有点遗憾,但也是做出来了。至少没白费这几小时的时间吧(笑)
开始
开始游戏。首先尝试用 JEB 读一下:
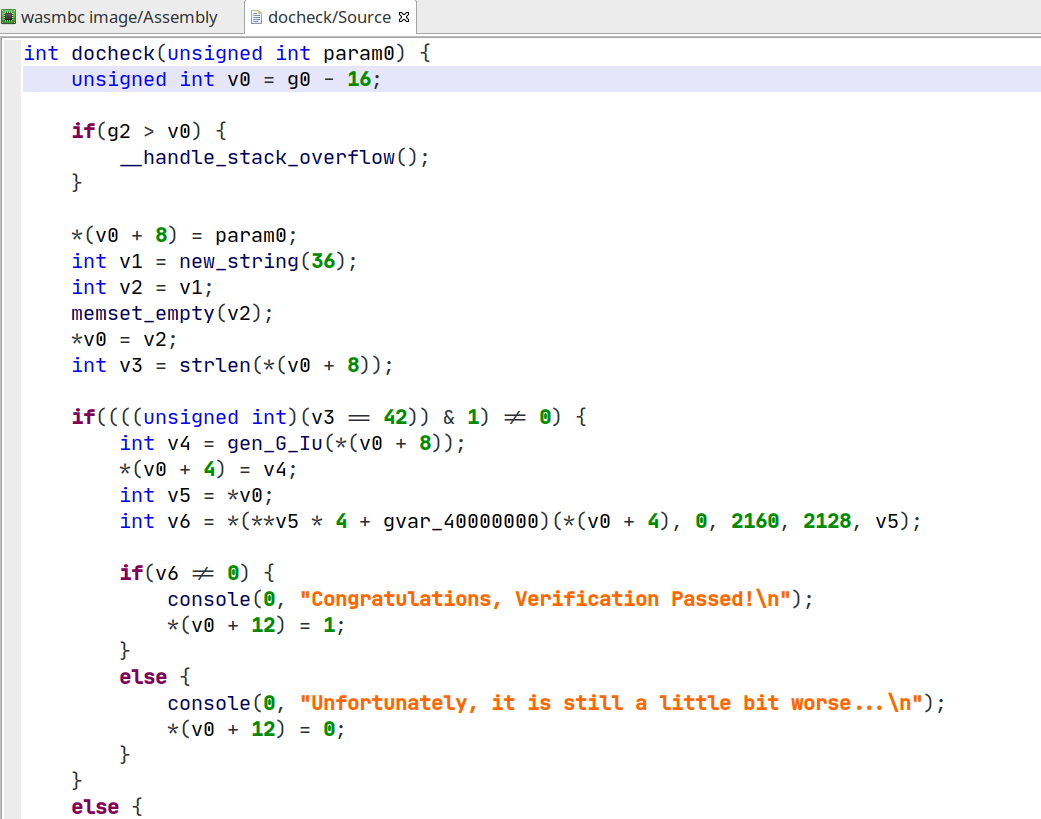
可以看到,逻辑还是非常清楚的(部分函数名为手动替换)。但美中不足的是对最关键的 f8 和 f9 不能查看伪代码,好像是 br_table 没做好,因此只能暂时放弃(
在等待了一段时间后,群里出现了 wasm2c 编译得到的 hello.o 文件。于是决定到 Windows 下用 F5 一战——
f9(base64)
f9 这个函数有超级明显的特征,就是这个字符串:

这东西过于 base64 了,甚至最后的 + 和 / 都完全一致。其得到结果的长度在动态调试下也和 base64 的一致,这就很有趣了。我们借助 IDA 的 F5 来看。首先是没进入循环的初始化部分:
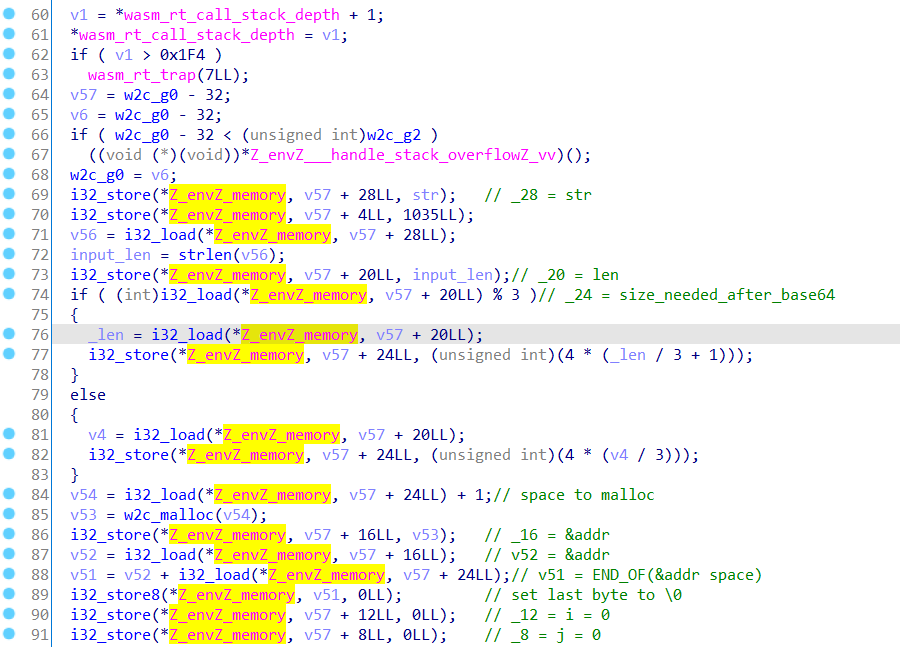
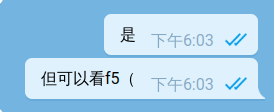
注意到 72 行有一个 strlen 函数。这个函数并不是 IDA 读出来的,而是在动态调试中试出来的。这里也有一个经验谈吧,就是以字符串为输入的 WASM 程序中基本都会有一个用来计算字符串长度的函数。
接下来的 74-83 行是和 3 有关的数学运算。这里就是 base64 的长度计算了:当整除 3 时即为 /3*4,当不整除时要多补 4 位。
然后是分配内存,并且将内存空间的最后一位置 \0,最后则是将两个数据置了 0。这里又是一个经验谈,在这种地方初始化成 0 的一般都是循环里面用到的变量。所以在这里简单将其命名为 i 和 j。
看完了初始化的部分,我们来看下面的循环:

首先是跳出循环的条件,姑且看懂就好。由于我们猜测这个函数和 base64 有较大关联,因此主要要做的就是代码,并与 base64 的源码进行比对。最先完成的是 addr[i] 的部分。

然后如法炮制,可以得到 addr[i+1]、addr[i+2] 和 addr[i+3] 的部分。

循环最后是对循环变量的处理。到此,接下来的部分基本不需要看了。我们整理一下上面的逻辑,可以写出 C 的对应伪代码:
char* encode(char* str) { char* addr; int len;
int i = 0, j = 0; while (1) { if (i >= addr + len - 2) { break; }
addr[i] = table[str[j] >> 2] ^ 0xa; addr[i + 1] = table[((str[j] & 3) << 4) | (str[j+1] >> 4)] ^ 0xb; addr[i + 2] = table[((str[j+1] & 0xf) << 2) | (str[j+2] >> 6)] ^ 0xc; addr[i + 3] = table[str[j+2] & 0x3f] ^ 0xd;
i += 4; j += 3; } return addr;}对比 base64 的 C 语言实现[1]:
unsigned int b64_encode(const unsigned char* in, unsigned int in_len, unsigned char* out) {
unsigned int i=0, j=0, k=0, s[3];
for (i=0;i<in_len;i++) { s[j++]=*(in+i); if (j==3) { out[k+0] = b64_chr[ (s[0]&255)>>2 ]; out[k+1] = b64_chr[ ((s[0]&0x03)<<4)+((s[1]&0xF0)>>4) ]; out[k+2] = b64_chr[ ((s[1]&0x0F)<<2)+((s[2]&0xC0)>>6) ]; out[k+3] = b64_chr[ s[2]&0x3F ]; j=0; k+=4; } }
if (j) { if (j==1) s[1] = 0; out[k+0] = b64_chr[ (s[0]&255)>>2 ]; out[k+1] = b64_chr[ ((s[0]&0x03)<<4)+((s[1]&0xF0)>>4) ]; if (j==2) out[k+2] = b64_chr[ ((s[1]&0x0F)<<2) ]; else out[k+2] = '='; out[k+3] = '='; k+=4; }
out[k] = '\0';
return k;}可以看到,其和标准 base64 实现的唯一区别就是对每一位都进行了一次异或。到此,f9 解析完成。
f8(主逻辑)
f8 的逻辑就复杂多了,不过也不是无迹可寻。看着复杂的代码分解到每个小部分却又各自非常简单,这就是 f8 的状况。
循环之前
我们首先来看进入循环之前的代码。

这里涉及到了大量对 u_addr 内存的操作。这里可以偷个懒,在初始化完成后的地方打上断点,然后把对应内存的内容复制出来:
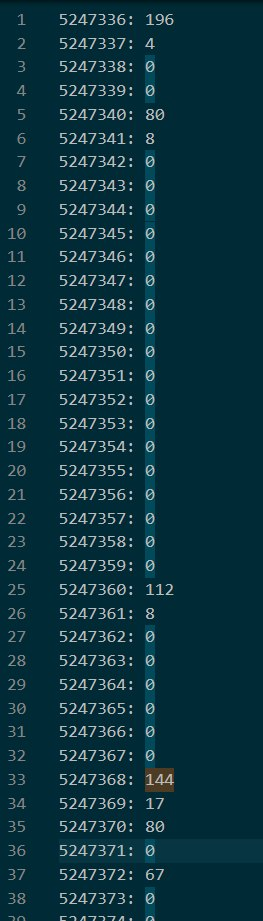
简单整理一下对应 offset 的实际内容:
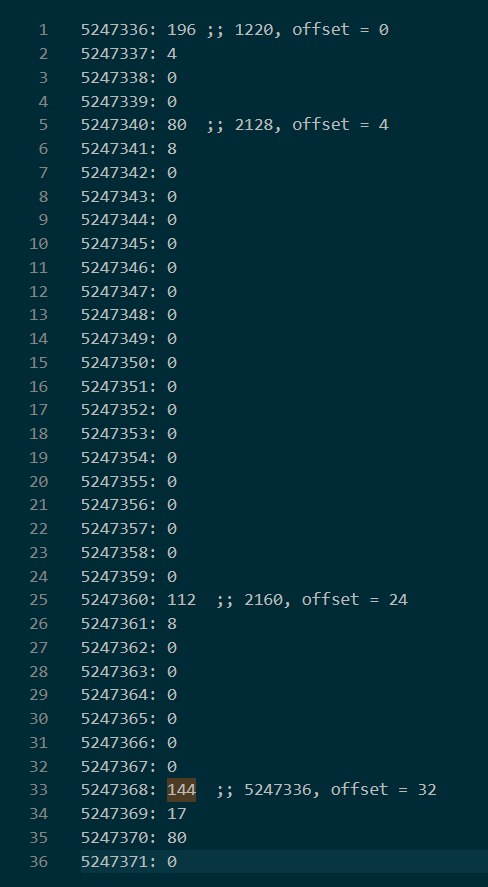
可以看到 2128 和 2160 分别被存储在了 offset = 4 和 offset = 24,而经过 base64 的数据则是存储在了 offset = 32 。
循环过程:初探
面对这样一个循环谁都头大。由于循环内是一个巨大的 switch,因此我简单跟踪了一下每次 switch 的取值:
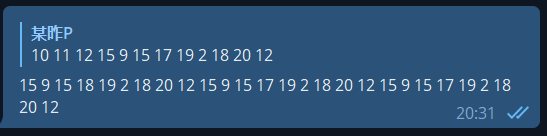
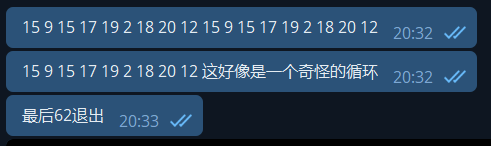
中间发现了一个循环,于是猜测了一下:
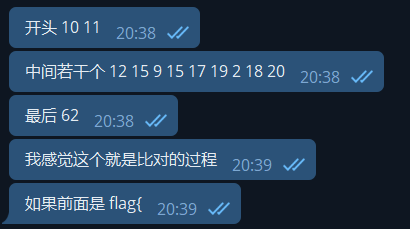
循环过程:函数对应
观察每个 switch 分支,可以看到他们都是 call_indirect 调用函数:

这部分可能在 IDA 里观察不大明显,但动态调试跟进去就很直观了。这个技巧在当时逆向 SC 的时候也用到了。
经过简单对比,我们发现:
于是省下了 114514 秒的动态调试时间(
循环过程:逻辑分析
这个过程就是单纯的分析那一连串函数的时间了,总体耗时约 40 分钟。最终得到这样一张图:
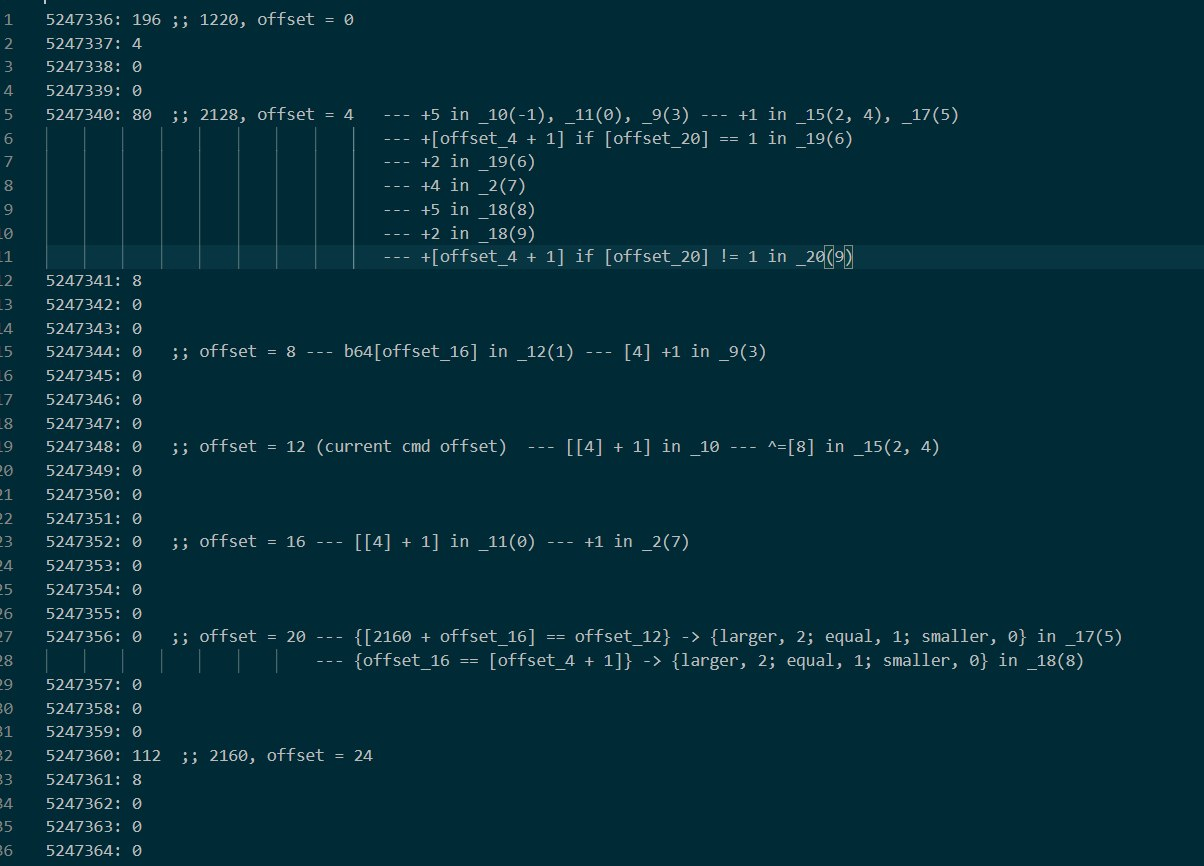
其中 _ 开头的表示调用函数,括号内是这个函数执行的顺序。
整理出这样的逻辑后,仔细观察。可以发现,整个比对是基于异或的。在 offset = 20 赋值的比对中,第一次比对应该是实际的数值比对。这次比对比较的是 base64 的值和 offset = 12 处的值,而这处的值经过了两次异或。这也就是最基本的逻辑了。
再整理一下,这张图可以修订成这样:
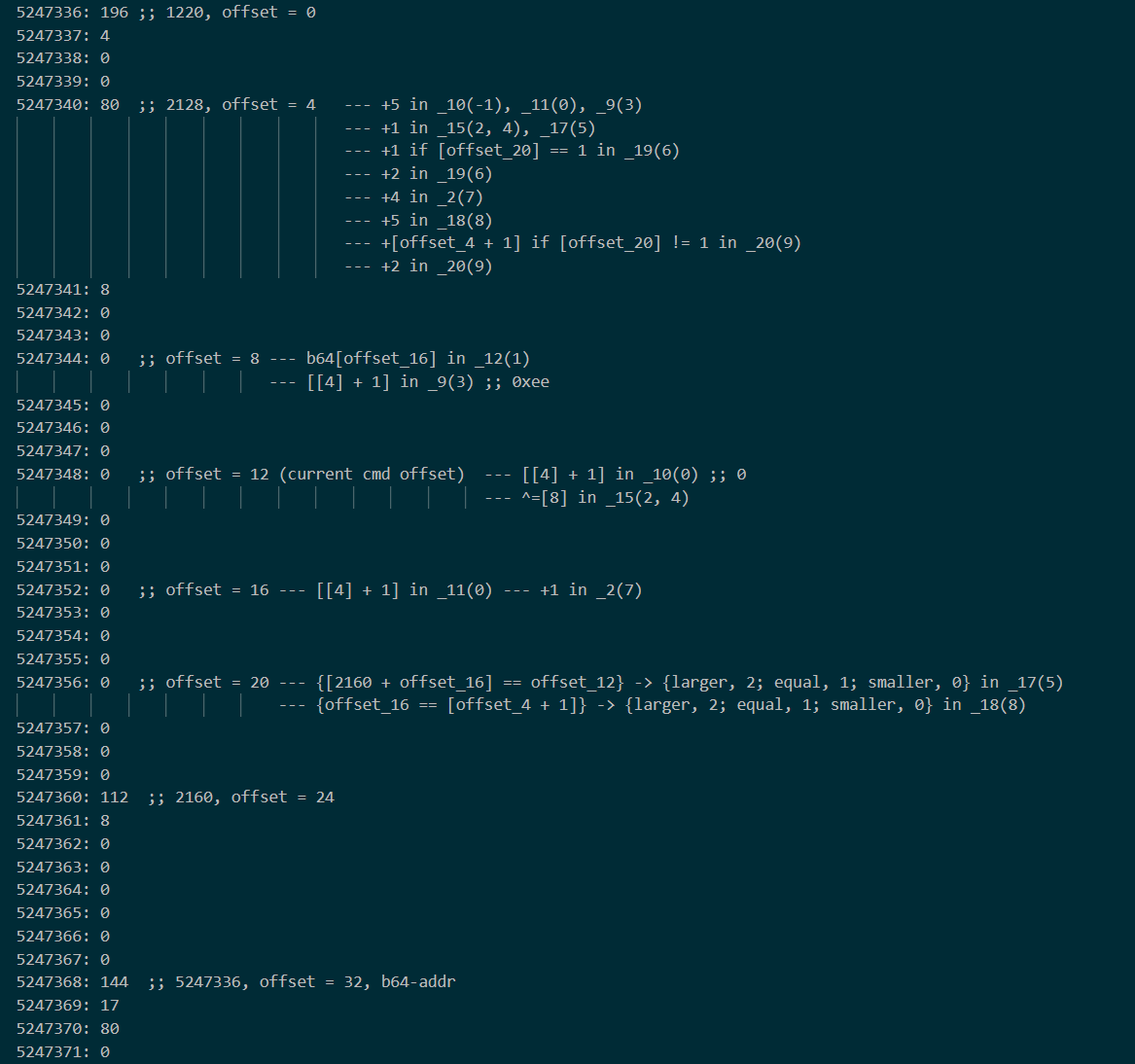
可以看到,offset = 12 处的值在最初被赋为 0,然后经过两次异或。第一次异或是 base64 对应偏移的内容,而第二次则是 0xee。
循环过程:逻辑整理
令输入数组为 b64,加密后数组为 data,当前位下标为 i,我们可以得到如下结论:
\mathtt{b64}_0\oplus\mathtt{0xee}=\mathtt{data}_0 \\\mathtt{b64}_0\oplus\mathtt{0xee}\oplus\mathtt{b64}_1\oplus\mathtt{0xee}=\mathtt{data}_1假设输入正确,则可以得到:
\mathtt{data}_{i-1}\oplus\mathtt{b64}_i\oplus\mathtt{0xee}=\mathtt{data}_i即:
\mathtt{b64}_0=\mathtt{data}_0\oplus\mathtt{0xee} \\\mathtt{b64}_i=\mathtt{data}_i\oplus\mathtt{data}_{i-1}\oplus\mathtt{0xee}解密
最终的脚本如下:
data = `0xbe60xac'0x99O0xdeD0xee_0xda0x0b0xb50x170xb8h0xc2N0x9cJ0xe1C0xf00x220x8a;0x88[0xe5T0xffh0xd5g0xd40x060xad0x0b0xd8P0xf9X0xe0o0xc5J0xfd/0x8460x85R0xfbs0xd70x0d0xe3` .split("\n") .map(t => (t.length === 1 ? t.charCodeAt() : Number(t)));
b64 = data .map((d, i) => (i == 0 ? d : d ^ data[i - 1])) .map(t => t ^ 0xee) .map((t, i) => { switch (i % 4) { case 0: return t ^ 0xa; case 1: return t ^ 0xb; case 2: return t ^ 0xc; case 3: return t ^ 0xd; } }) .map(t => String.fromCharCode(t)) .join("");
atob(b64);后记
从这题开始我开始尝试用 IDA 分析 WASM。看过我之前博客(包括加密的两篇 SC)的读者应该知道,我之前都是直接分析 wat 的。但在 wat 行数不断增加的当下,我们也需要快速分析的手段。
JEB 分析很好用,但对于有些代码没办法成伪代码;IDA 配合 F5 也可一用,但混杂了大量无用的代码需要手动去除;Chrome 的动态调试是神,虽然还有不大好用的地方,但能大幅简化分析的难度;WAT 的阅读是基本功,只要会读 WAT,那么逆向 WASM 只是时间问题。
嘛,就是这样(逃