贝塞尔曲线、字体矢量化与曲线运算

这篇文章总共探讨三个内容，正如标题所述：贝塞尔曲线、字体矢量化是假的与曲线运算。然而，实际上这三个问题是同一个问题，都是围绕着贝塞尔曲线展开的。而对贝塞尔曲线进行处理也可以得到很多有趣的有用的结果。

贝塞尔曲线

贝塞尔曲线是在 ASS 绘图代码、矢量作图、乃至字体设计中都广泛应用的一种曲线，比如 InkScape 的 Path 绘制：

基本概念

我们将整条贝塞尔曲线用表达式 $\bold{B}(t)$ 表示，其中 $t\in[0,1]$ 。

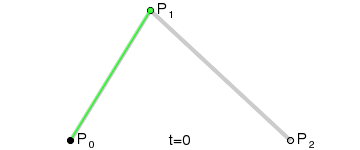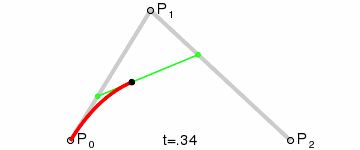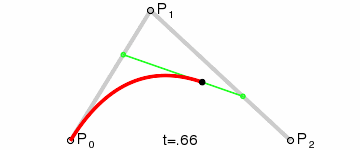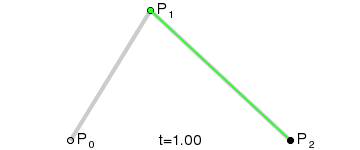
从单纯的语义上来看，t 可以代表曲线描绘的进程。这种“进程感”在看曲线描绘的动图的时候可能更加明显一些，我们来看下面这张二阶贝塞尔曲线的绘画过程图：

https://upload.wikimedia.org/wikipedia/commons/3/3d/B%C3%A9zier_2_big.gif

注意下面的数字，在等号 = 后面其实还有一个小数点（.），因此数字是从 0 ~ 1 不断递增的。而随着数字的不断递增，曲线也在被不断描绘，最后当 $t=1$ 时，曲线描绘完成。

我们发现，图中出现了三个点： $\bold{P}_0$ 、 $\bold{P}_1$ 和 $\bold{P}_2$ 。我们将这三个点称为控制点，因为这三个点控制并决定了这条曲线的具体形状。

我们将曲线上的某一时刻的点用 $\bold{B}$ 表示，不难发现 $\bold{B}$ 的位置和 $\bold{P}_0$ 、 $\bold{P}_1$ 、 $\bold{P}_2$ 三个点息息相关。那二者究竟是什么关系呢？

我们依然来看上面这张动图，仔细观察不断移动的各个圆点的位置和 $t$ 的关系，不难发现圆点的位置其实就相当于 $\bold{P}_0$ 和 $\bold{P}_1$ 之间的 $t$ 处。比如当 $t=0.1$ 时， $\bold{P}_0$ 和 $\bold{P}_1$ 之间的圆点就位于 $\bold{P}_0$ 出发后十分之一处； $\bold{P}_1$ 和 $\bold{P}_2$ 之间的圆点也是如此。在确定了这两个圆点之后，我们在这两个圆点连成的线上同样找到 t 的位置，对应的那个位置就是点 B 的所在了。

控制点与阶数

上面的介绍中我们不断地提到了“二阶贝塞尔曲线”这个概念，那阶数和控制点的数量又有着什么样的关联呢？其实我觉得这个问题大家心里已经有答案了（

对于贝塞尔曲线而言，最关键的就是控制点，而其阶数也和控制点的数量息息相关。当只有两个控制点时，贝塞尔曲线其实就相当于这两个点的连线，描绘这条曲线的过程也就相当于在两点之间线性插值的过程，因此被称为线性贝塞尔曲线；当存在三个控制点时，这样的贝塞尔曲线被称为二阶贝塞尔曲线；随着控制点数量的不断增多，我们能做到的对曲线的控制也就更加精细，能够绘制出的曲线形状也就更加自由。

于是在这里我们可以得到：贝塞尔曲线的阶数 = 控制点的数量 - 1。

高阶贝塞尔曲线

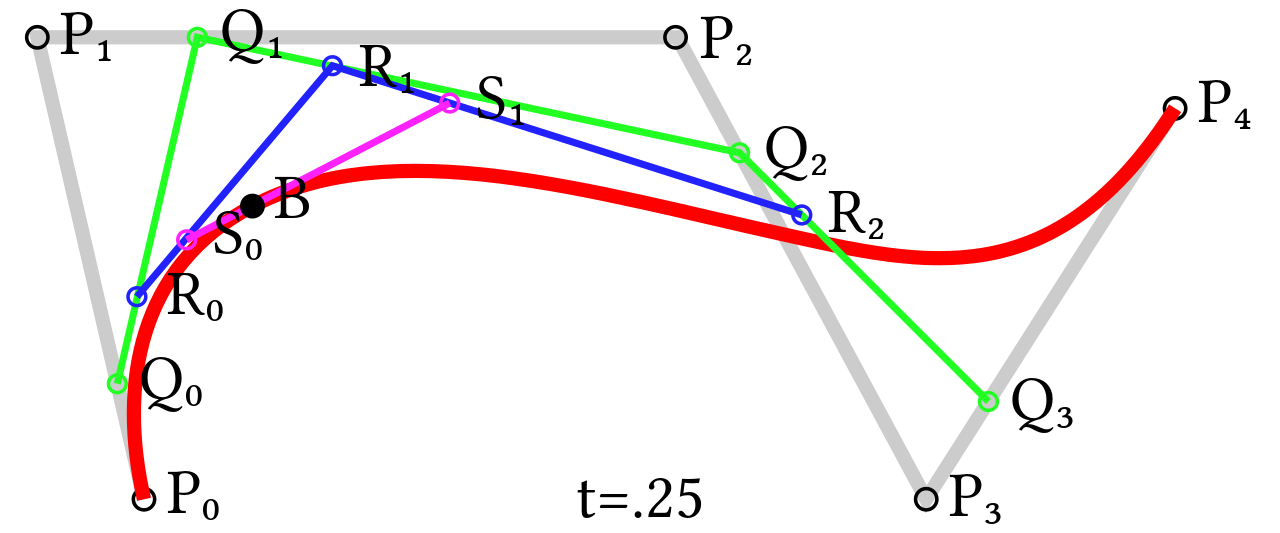
下面我们来看个稍微复杂点的例子。这是一张四阶贝塞尔曲线的绘画过程图， $t=0.25$ ，如下图所示：

https://upload.wikimedia.org/wikipedia/commons/thumb/b/bf/B%C3%A9zier_4_big.svg

可以看到，相对于二阶贝塞尔曲线，四阶就要复杂一些了，但依然是万变不离其宗。

首先依然是将各控制点 $P$ 按顺序依次连成线，可以看到各个 $P$ 点之间是用灰线连接的。

然后是确定各个 $Q$ 点的位置，并将 $Q$ 点也依次连接起来，图中使用的是绿色表示。

第三步是将各个 $R$ 点的位置确定，同样依次连接，见图中的蓝线。

最后，我们发现：蓝线只有两条。那这时将蓝线上的 $S$ 点位置确定，然后在 $S$ 点连线上根据 $t$ 就可以得到我们想要的 $B$ 点了。

可以看出，每经过一步，连线的数量就会减少 1。到最后只剩下一条线时，在这条线上确定的 $t$ 的位置就是 $\bold{B}(t)$ 对应的点了。

`n` 阶贝塞尔曲线的代数定义

从代数上来看，贝塞尔曲线其实是由下面这个式子生成的（其中 n 代表曲线的阶数）：

\bold{B}(t)=\sum\limits_{i=0}^{n}{\left(\begin{matrix}n \\ i\end{matrix}\right)\bold{P}_i(1-t)^{n-i}t^i}​

其中 $n$ 代表曲线的阶数，而 $\bold{P}_i$ 则代表第 $i$ 个控制点。 $\bold{P}_0$ 代表起点控制点，而 $\bold{P}_{n-1}$ 代表终点控制点。

字体矢量化

其实说字体矢量化是个伪命题，因为我们现在使用的字体大多本身就是矢量字体，矢量图形本身又何来矢量化一说呢（笑）？所以这个标题也只是为了引出这个事实罢了其实是我想不出别的标题了（逃。

以这个 あ 为例，这里我们选用的字体是文泉驿正黑体，使用的软件是 FontForge。限于屏幕高度原因，这里无法将整个字截下，故上部会有所遮挡。

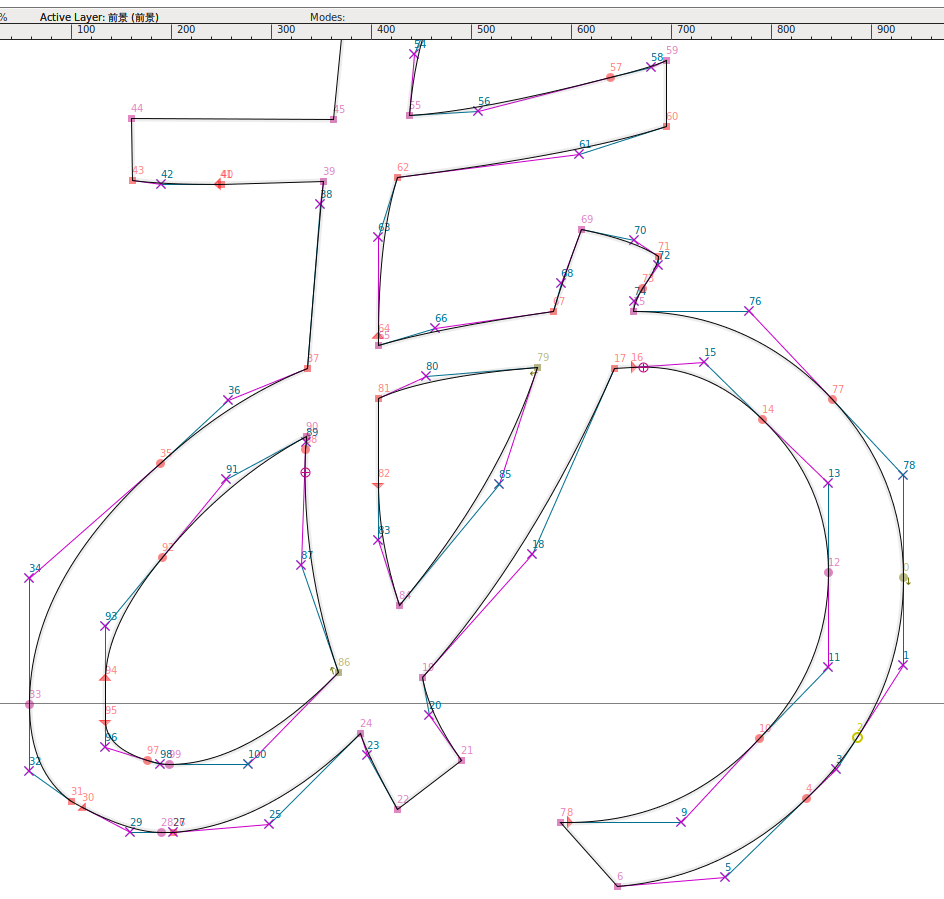
这里我们可以看到很多有着各种含义的标号。这里我建议各位真的有各位吗去简单阅读一下这篇关于 FontForge 使用的介绍文档[3]。

我们需要了解的就是中间的 X 符号，这代表的就是贝塞尔曲线中间的控制点，而位于 X 左右的的圆点则代表贝塞尔曲线的起始控制点。可以看到，整个字中存在着大量的 X 号，而每一个 X 就代表着一条二阶贝塞尔曲线。

为什么说是二阶贝塞尔曲线呢？因为 TrueType 字体在构建后就只剩下二阶贝塞尔曲线了，而我们使用的也正是发行的字体，因此图中出现的也就都是二阶贝塞尔曲线了。

在本章中，我们只讨论三阶路径，它在绘制字形时普遍使用。Spiro 路径将在下一章讨论，二阶曲线在绘制时很少用到，只会在 TrueType 字体中找到 — 他们更常出现在构建时.

FontForge 与字体设计 - 理解Bézier曲线 [3]

除去贝塞尔曲线之外，描绘字体的也就只剩下了直线（l），移动位置（m）和闭合曲线（通常可以用 m 直接代替）。而这些都能在 ASS 的绘图指令中找到对应。这也就是字体可以转化成绘图指令——也就是所谓的字体“矢量化”之名出现的原因了。

曲线运算

说是运算，其实也就只有两种：化直为曲和曲线分割。

化直为曲

我们知道，贝塞尔曲线是可以完美表示直线的，也就是上面提到的线性贝塞尔曲线。但当我们需要使用 n 阶贝塞尔曲线表现直线的时候又该怎么办呢？

其实也很简单，只要让中间的控制点位于起止点的连线上就可以了。这个原理也很好想明白，大家可以想想看（笑）

于是我这里用 JavaScript 简单实现了一下，看看就好（：

1
function l2b(start = [0, 0], end = [0, 0]) {
2
  return [
3
    start,
4
    [start[0] + (end[0] - start[0]) / 3, start[1] + (end[1] - start[1]) / 3],
5
    [
6
      start[0] + ((end[0] - start[0]) / 3) * 2,
7
      start[1] + ((end[1] - start[1]) / 3) * 2,
8
    ],
9
    end,
10
  ];
11
}

曲线分割

结论

此处以三阶贝塞尔曲线为例。

如果我们想要在 $t=k$ 处截断 $\bold{B}(t)$ ，那原曲线就相当于被拆成了左右两个部分。

我们知道： $\bold{P_0}$ 、 $\bold{P_1}$ 、 $\bold{P_2}$ 和 $\bold{P_3}$ 是最开始的四个定位点，而接下来我们需要确定的是作图第一步确定的三个点 $\bold{Q_0}$ 、 $\bold{Q_1}$ 和 $\bold{Q_2}$ :

\begin{aligned} \bold{Q_0}=(1-k)\bold{P_0}+k\bold{P_1} \\ \bold{Q_1}=(1-k)\bold{P_1}+k\bold{P_2} \\ \bold{Q_2}=(1-k)\bold{P_2}+k\bold{P_3} \\ \end{aligned}

然后，我们确定接下来的两个点 $\bold{R_0}$ 和 $\bold{R_1}$ ：

\begin{aligned} \bold{R_0}&=(1-k)\bold{Q_0}+k\bold{Q_1} \\ &=(1-k)((1-k)\bold{P_0}+k\bold{P_1})+k((1-k)\bold{P_1}+k\bold{P_2}) \\ &=(\bold{P_0}-2\bold{P_1}+\bold{P_2})k^2+(2\bold{P_1}-2\bold{P_0})k+\bold{P_0} \\ \bold{R_1}&=(1-k)\bold{Q_1}+k\bold{Q_2} \\ &=(1-k)((1-k)\bold{P_1}+k\bold{P_2})+k((1-k)\bold{P_2}+k\bold{P_3}) \\ &=(\bold{P_1}-2\bold{P_2}+\bold{P_3})k^2+(2\bold{P_2}-2\bold{P_1})k+\bold{P_1} \end{aligned}

最后，我们可以得到 $\bold{B}$ ：

\begin{aligned} \bold{B}&=(1-k)\bold{R_0}+k\bold{R_1} \\ &=(1-k)((\bold{P_0}-2\bold{P_1}+\bold{P_2})k^2+(2\bold{P_1}-2\bold{P_0})k+\bold{P_0})+k((\bold{P_1}-2\bold{P_2}+\bold{P_3})k^2+(2\bold{P_2}-2\bold{P_1})k+\bold{P_1}) \\ &=(-\bold{P_0}+3\bold{P_1}-3\bold{P_2}+\bold{P_3})k^3+(3\bold{P_0}-6\bold{P_1}+3\bold{P_2})k^2+(-3\bold{P_0}+3\bold{P_1})k+\bold{P_0} \end{aligned}

我们的结论是：左半边的曲线可以用 $\bold{P_0}-\bold{Q_0}-\bold{R_0}-\bold{B}$ 这四个定位点表示，而右半边的曲线可以用 $\bold{B}-\bold{R_1}-\bold{Q_2}-\bold{P_3}$ 表示。

证明

下面我们来证明这个结论。我们先来看三阶贝塞尔曲线的多项式展开：（1）

\begin{aligned} \bold{B}(t)&=(1-t)^3\bold{P_0}+3t(1-t)^2\bold{P_1}+3t^2(1-t)\bold{P_2}+t^3\bold{P_3} \\ &= (1-3t+3t^2-t^3)\bold{P_0}+(3t-6t^2+3t^3)\bold{P_1}+(3t^2-3t^3)\bold{P_2}+t^3\bold{P_3} \\ &= (-\bold{P_0}+3\bold{P_1}-3\bold{P_2}+\bold{P_3})t^3+(3\bold{P_0}-6\bold{P_1}+3\bold{P_2})t^2+(-3\bold{P_0}+3\bold{P_1})t+\bold{P_0} \end{aligned}

将 $t$ 替换成 $kt$ ，多项式表示的就是 $t=k$ 截断处左半边的曲线：（2）

\begin{aligned} \bold{B}(kt)&= (-\bold{P_0}+3\bold{P_1}-3\bold{P_2}+\bold{P_3})k^3t^3+(3\bold{P_0}-6\bold{P_1}+3\bold{P_2})k^2t^2+(-3\bold{P_0}+3\bold{P_1})kt+\bold{P_0} \end{aligned}

此时，由于 $t\in[0, 1]$ ，而 $k$ 是常数，因此 $kt\in[0, k]$ ，符合曲线左半边的定义域要求。

而而将 $\bold{P_0}-\bold{Q_0}-\bold{R_0}-\bold{B}$ 这四个定位点代入（1）式的 $\bold{P_0}$ 、 $\bold{P_1}$ 、 $\bold{P_2}$ 和 $\bold{P_3}$ 中：（3）

\begin{aligned} \bold{B}(t)&=(1-3t+3t^2-t^3)\bold{P_0}+(3t-6t^2+3t^3)\bold{Q_0}+(3t^2-3t^3)\bold{R_0}+t^3\bold{B} \\ &=(1-3t+3t^2-t^3)\bold{P_0} \\ &+(3t-6t^2+3t^3)((1-k)\bold{P_0}+k\bold{P_1}) \\ &+(3t^2-3t^3)((\bold{P_0}-2\bold{P_1}+\bold{P_2})k^2+(2\bold{P_1}-2\bold{P_0})k+\bold{P_0}) \\ &+t^3((-\bold{P_0}+3\bold{P_1}-3\bold{P_2}+\bold{P_3})k^3+(3\bold{P_0}-6\bold{P_1}+3\bold{P_2})k^2+(-3\bold{P_0}+3\bold{P_1})k+\bold{P_0}) \\ &=(-\bold{P_0}+3\bold{P_1}-3\bold{P_2}+\bold{P_3})k^3t^3+(3\bold{P_0}-6\bold{P_1}+3\bold{P_2})k^2t^2+(-3\bold{P_0}+3\bold{P_1})kt+\bold{P_0} = \bold{B}(kt) \end{aligned}

（1）、（3）式相等，故左半边的曲线可以用 $\bold{P_0}-\bold{Q_0}-\bold{R_0}-\bold{B}$ 这四个定位点表示。

同理，可证右半边的曲线可以用 $\bold{B}-\bold{R_1}-\bold{Q_2}-\bold{P_3}$ 表示。

你也可以使用下面这个脚本在 Octave 中验证这个结论：

1
pkg load symbolic
2

3
syms k t P0 P1 P2 P3
4

5
function retval = bezier(t, p0, p1, p2, p3)
6
  expr = (1-t)^3*p0+3*t*(1-t)^2*p1+3*t^2*(1-t)*p2+t^3*p3
7
  retval = expand(expr)
8
endfunction
9

10
function ret = next(k, p0, p1)
11
  ret = expand((1-k)*p0+k*p1)
12
endfunction
13

14

15
# points
16
Q0=next(k, P0, P1)
17
Q1=next(k, P1, P2)
18
Q2=next(k, P2, P3)
19
R0=next(k, Q0, Q1)
20
R1=next(k, Q1, Q2)
21
B=next(k, R0, R1)
22

23
# left
24
left=bezier(k*t, P0, P1, P2, P3)
25
left_divided=bezier(t, P0, Q0, R0, B)
26
left == left_divided
27

28
# right
29
right=bezier(k+(1-k)*t, P0, P1, P2, P3)
30
right_divided=bezier(t, B, R1, Q2, P3)
31
right == right_divided

这种分割方式也适用于更高阶的贝塞尔曲线。

图示

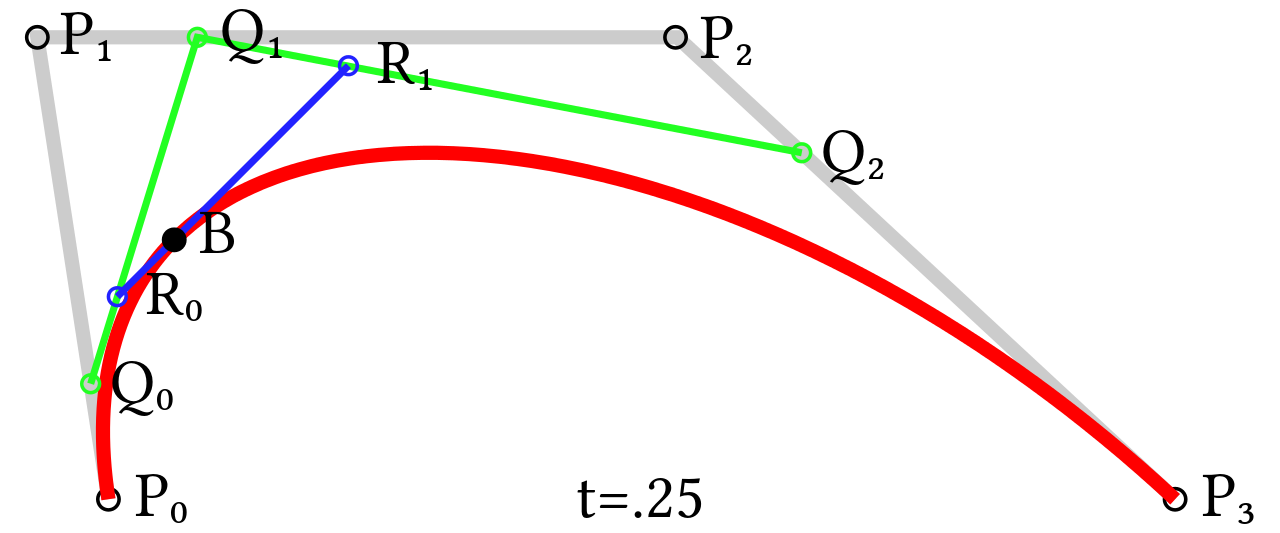
既然上面是用的三阶贝塞尔曲线举例，那我就找一张三阶的图好了：

https://upload.wikimedia.org/wikipedia/commons/thumb/8/89/B%C3%A9zier_3_big.svg/1280px-B%C3%A9zier_3_big.svg.png

可以看到，上面我们得出结论的 $\bold{P_0}-\bold{Q_0}-\bold{R_0}-\bold{B}$ 恰好就是 $\bold{B}$ 左边的三个点加上 $\bold{B}$ ；而 $\bold{B}-\bold{R_1}-\bold{Q_2}-\bold{P_3}$ 也恰好是 $\bold{B}$ 加上 $\bold{B}$ 右边三个点。

因此，当你一时想不起分割原理的时候，画一张这样的图就可以了（笑）

简单代码实现

这里简单用 JavaScript 实现了一个中点分割，还是看看就好（笑）：

1
function splitB(start = [0, 0], p1 = [0, 0], p2 = [0, 0], p3 = [0, 0]) {
2
  function average(a = [0, 0], b = [0, 0]) {
3
    return [(a[0] + b[0]) / 2, (a[1] + b[1]) / 2];
4
  }
5

6
  const m0 = average(start, p1);
7
  const m1 = average(p1, p2);
8
  const m2 = average(p2, p3);
9

10
  const q0 = average(m0, m1);
11
  const q1 = average(m1, m2);
12

13
  const b = average(q0, q1);
14

15
  return [
16
    [start, m0, q0, b],
17
    [b, q1, m2, p3],
18
  ];
19
}

结语

万万没想到的是写这样一篇文章用去了我整整一天的时间。问题的一切是从字体形变开始的，了解贝塞尔曲线只是试图实现这个效果中的第一步罢了。

贝塞尔曲线这方面的问题其实就是纯粹的数学问题，一句话概括就是多项式被离散数学支配的恐惧；而矢量字体这件事情则是被我完全忘记了，直到用 FontForge 看字形之后才反应过来。

分割贝塞尔曲线之后就可以做很多事情了，比如更精细地绘制图形，又或者是其他的各种需求，不过这都是后话了（笑）

贝塞尔曲线、字体矢量化与曲线运算

ToC